Quantum computing has received a lot of attention in the past years and in fall 2019 Google claimed they achieved the so-called quantum supremacy. Quantum computing brings with it great promises from its early days, when Richard Feynman and others, imagined that leveraging the quantum properties of subatomic particles could lead to devices with inconmensurable computing power compared to what could be ever achieved with a classical computer.

I am no quantum researcher or expert, I cannot reasonably predict who is going to win this “race” for quantum supremacy or even when. However, these recent claims make the race even more exciting to watch. Even if a usable quantum computing chip does not seem to be something we will have at hand in the short term, there is still a lot that can be done now, with simulations for instance.
Among the big players, Microsoft made an interesting move. Indeed, they started building an “open quantum programming community” by releasing end of 2017 their Q# programming language.
Microsoft describes Q# as:
Q# (Q-sharp) is a domain-specific programming language used for expressing quantum algorithms. It is to be used for writing subroutines that execute on an adjunct quantum processor, under the control of a classical host program and computer. Until quantum processors are widely available, Q# subroutines execute on a simulator.
Actually, Microsoft released a full Quantum Development Kit on top of the Q# compiler. It is completely free and open source. Following Microsoft habits to do things properly, even in its early days this was really well polished: documentation was pretty neat and complete and even some samples were shipped to help you start. They did pretty good job making all this super attractive, even the name Q# sounds cool, doesn’t it?
I started playing around with Q# in spring 2018. I managed to install and ran the provided samples (on my Mac) without any trouble. However, after all this I felt a little stuck. Now so what? Crafting quantum algorithms on my own seemed to be a distant dream, so I stopped there for a couple of months. It seems that the Microsoft QuArc team noticed this lack of training programs and guidance. To overcome this they launched end of 2018 the Quantum Katas: a series of exercises and tutorials so that “newbies” like me could ramp up at their own pace. It is really well done: very didacting and complete. I definitely recommend this as #1 source for anyone who would like to get started with quantum computing and programming.
In this blog post, I share some of my feedbacks, tips and even resources to help you getting started. As discussed here, to start for real quantum computing you need higher (post-secondary) education in mathematics. However, you can definitely get the substance of what is quantum computing with no maths at all. In all cases, I recommend you this 3-minutes videos, for a quick overview of what quantum computing is.
An overview of Quantum Katas

Quantum Katas is a series of tutorials and exercises provided by Microsoft. They come with the form of small challenges that you need to solve using the Q# programming language. They guide you progressively from the very beginning to advanced and hard problems on quantum computing.
Most of the katas are presented as a Q# operation whose implementation is missing and your job is to complete it. Similarly to a unit test, the quantum simulator will validate your submission on a series of test inputs (that is left unknown to the programmer). Usually, completing a kata does not take more than 20 lines of Q# at max.
When executed within a Jupyter notebook, you benefit from well formatted explanations with beautiful maths equations right next to your Q# code inputs.
What are the real prerequisites to get started with Q# and Quantum Katas?
On the Katas’s webpage Microsoft provides the prerequisites to get started. I think it was interesting to provide my point of view here.
Mathematics
Linear algebra is almost everywhere in quantum computing. Precisely, linear algebra with the field $\mathbb{C}$ of complex numbers. As you will learn, a $N$-Qubits system is described by a $2^{N}$ dimensional vector space on $\mathbb{C}$.
I would say that to really get started with quantum computing, one would need a good knowledge on complex numbers and linear algebra that would correspond more or less to a BSc. in Sciences. In the french/european universitarian system this corresponds to Licence L2/L3 or Maths Spé (for preparation classes). I was a maths teaching assistant at University Paris VI for three years, I taught there linear algebra, material and exercices are still available here (in french).
The Quantum Katas provide two tutorials about complex numbers and linear algebra. Yet, in my humble opinion, I think this a good refresher on concepts and notations but I doubt one can reasonably learn from scratch and be ready for the rest of Quantum Katas.
Programming
At first glance, the Q# syntax looks like C# syntax. Moreover, Q# is functional by design and one can definitely see inspiration from F#, the C# cousin’s functional language, also running on top of the .NET CLI. For example, variables are immutable by default. But do not worry too much, your interaction with .NET will be limited to the sole installation of .NET Core on your machine (maybe not at all if you go with a Docker install).
This is how a piece of Q# looks like. Similarly to its great cousins: F# and C#, it let you switch easily between functional and imperative styles.
When completing Quantum Katas, you will not be required to go really deep in the Q# language. Most of the exercices are solved with a couples of lines. To do your katas, you will just have to learn the fundamentals of the language: basic syntax, types, loops, conditional statements and of course use the core of the Q# libraries for Qubits manipulations: Gates, Measurements, Simulations etc.
Contrary, to the maths prerequisites that are underestimated in Quantum Katas introduction, you absolutely do not need to be a hardcore programmer to get started with Q# and Quantum Katas.
Let us just point out that the Q# QDK is much more that just a mere Domain Specific Language (DSL) on top of the .NET CLI. It implements a rich type system and comes with an extensive library suite adapted to Quantum Programming. For example, operations are distinguished from functions. In addition, operations have advanced functors support such as adjoint and controlled version which makes this very impressive from a language design perspective. No doubt that there are great engineers and researchers at work in the QuArc Team. This also proves that this is a real investment for Microsoft, not just a toy to do some buzz.
Physics
Good news here: you do not necessarily need any previous knowledge on quantum mechanics to get started. Contrary to maths and computer science, I did not study quantum mechanics. I learned recently the basics.
I would recommend nevertheless some quick onboarding tour on the fundamental concepts on quantum mechanics (see the recommended resources below). Good news this is fascinating. I hope you will enjoy as much as I did.
Some tips and a compilation of good resources available on the web
While the Quantum Katas, and more generally the Microsoft documentation, point to a lot of great ressources. I thought that it would be interesting sharing what helped me the most.
Accept (quickly) the principles of quantum mechanics
Before you can start with quantum programming, you just need to accept some of the fundamentals of quantum mechanics: superposition and entanglement. I think that you do not need much more than this. I also chose the wording accept, on purpose. Pr Richard Feynman even said to his students:
If you think you understand quantum mechanics, you don't understand quantum mechanics.
So my advice here is to accept these principles and quick, otherwise you would be stuck there for a very long time. You will have plenty of time to meditate on this but if you want to start quantum computing this will slow you down. And, before I forget, let me also warn you with a common mistake, we beginners do to reassure ourselves when confronted with the shocking reality of quantum mechanics. It is tempting to think that a Qubit in superposition is still Zero or(exclusively) One but because we cannot observe it for some obscure reasons, it is just a modelisation of the possible outcomes by probabilities. That’s incorrect: with superposition, they are both $|0\rangle$ and $|1\rangle$ at the same time. Yes this is crazy! But there’s another world down there at subatomic scale, with different laws…
I also saw some amazing animations on this website (in French): toutestquantique.fr
From the same authors, this video illustrates well the wave-particle duality.
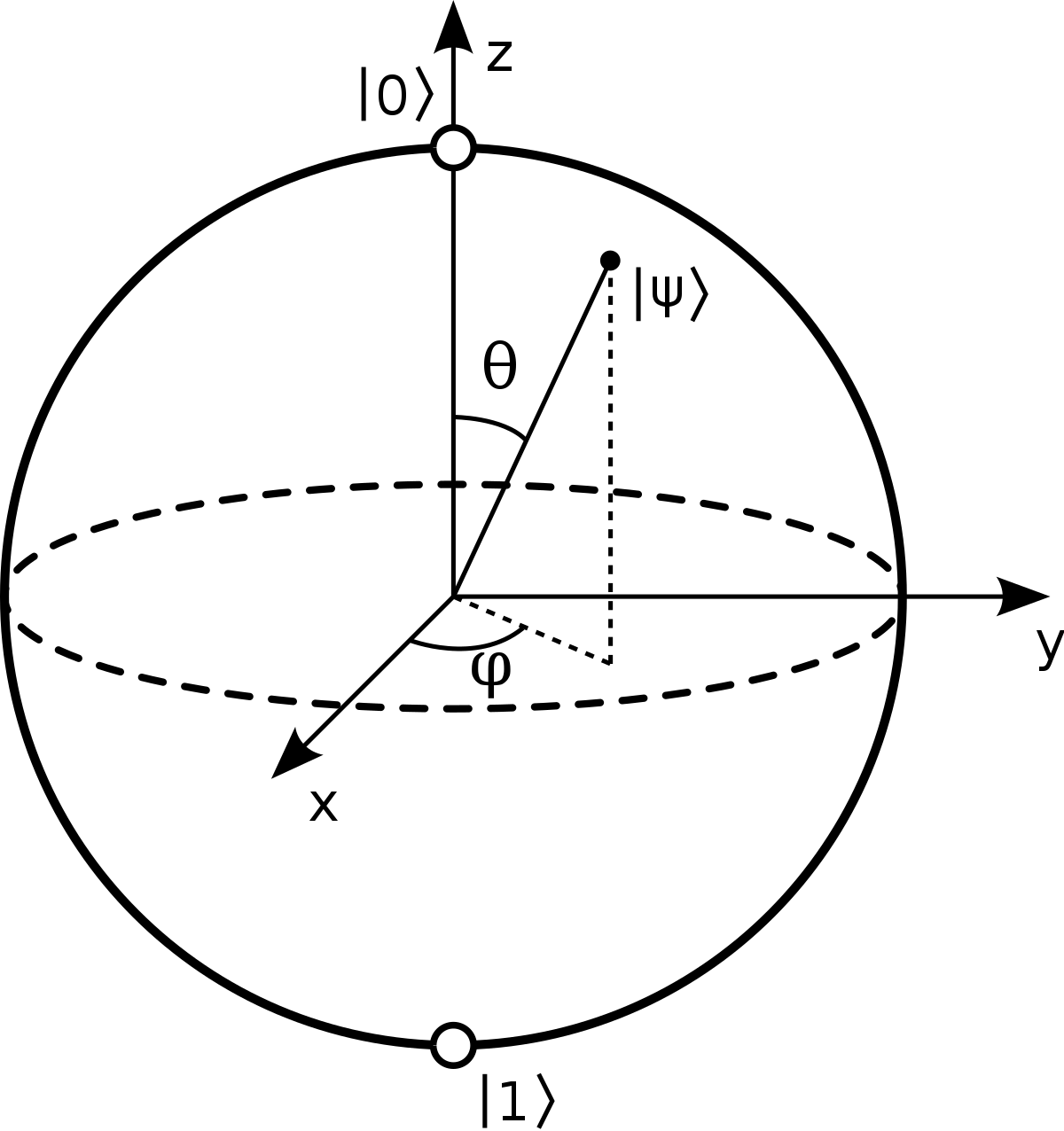
Do not spend too much time on the Bloch Sphere and quantum circuit visualizations
The Quantum Katas take an approach “by code” with Q#. This has been really adapted for me. But with other didactic approaches I followed when I started, the Bloch Sphere is often used to represent and visualize 1-Qubit states.
Indeed, a Qubit in the arbitrary (superposed) state $\ket{\psi}$ can be written $\alpha \ket{0} + \beta \ket{1}$, $\alpha, \beta \in \mathbb{C}$ but also $ cos(\frac{\theta}{2}) \ket{0} + e^{i\phi} sin(\frac{\theta}{2})\ket{1}$, $\theta, \phi \in \mathbb{R}$. This leads to a 3D visualization on the Bloch Sphere. I allows you to see the actions of the most commonly used 1-Qubit gates, such as Hadamard and Pauli gates.. However, again in my humble opinion with my little experience, this has not brought much to me to understand quantum computing and its concepts. In addition, keep in mind that this visualization is limited to 1-Qubit states. You will quickly manipulate multi Qubits systems so the Bloch sphere will not help you much there.
When starting to learn quantum computing, a reference often cited is Quirk. While it’s an amazing project, building visual quantum circuits has not really helped me to “get” the fundamentals of quantum computing and why it can achieve for example these exponential speed ups.
Adopt quickly the bra-ket notations and get used to tensorial product
If you come with a mathematical background you probably have not worked with bra-ket notations before. If everybody use them in quantum mechanics and computing this is for a reason. As you will learn in the Quantum Katas tutorials, the canonical base for a 3-Qubit systems is composed of the 8 vectors $\ket{000}$, $\ket{001}$, $\ket{010}$… which is much more handy to write compared to a $\mathbb{C}$ 8-dimensional vector for each. Remember, a $N$-Qubit state is represented by a $2^{N}$ dimensional vector. Convince yourself that the bra-ket notations are consistent with the matrix representation you are more familiar with and after that stick and embrace bra-ket notations. I also advise you to review the tensor product properties, which is used intensively in quantum computing. In my mathematical studies I had encountered it sometimes (more frequently as an exercise), here it plays a central role.
Watch this PhD comics video - 6min
This one is more advanced than the video mentioned in the introduction. Yet, it gives you an amazing tour on what quantum computing is in only 6 minutes.
Watch this conference from Andrew Helwer - 1h30
The conference is lead by a young talented researcher. With humility and great clarity, he onboards an audience of computer scientists to quantum computing. The attendees’ questions are also relevant.
Use Jupyter notebooks for your Quantum Katas
When completing Quantum Katas. You will have the choice to run them as Q# projects or Jupyter notebooks. I strongly encourage you to use the notebooks. You will benefit from great well formatted tutorials with $ \LaTeX $ formulas.
Quickly, Jupyter is a Python based opensource project which allows you to write code in cells embedded within a web page called a notebook. The code in cells is remotely executed by a webserver kernel. Here the Q# team distributed a Jupyter kernel: IQSharp, performing Q# execution for notebooks. This may sounds a little bit complicated but just follow the instructions to have this setup, you will not regret it.
By the way, I recommend installing Jupyter with pip and virtual environment. With Python, I am not a big fan of Conda and global installs and have always been a promoter of the use of virtual environments.
Understanding Deutsch–Jozsa is a good first objective
After following, the first tutorials and katas on Qubits, Superposition, Measurements etc. I strongly advise you to start with Deutsch-Jozsa algorithm. Even the problem it solves does not sound sexy, it is definitely the simplest example where quantum computing achieves an exponential speedup.
Shortly, it allows “with one oracle evaluation” to determine if a function $f: \lbrace 0, 1 \rbrace^{N} \rightarrow \lbrace 0, 1 \rbrace$ is either constant or balanced (output the same number of zeros and ones). With a classical computing you would need in the worst case $2^{N-1}+1$ evaluations but with Deutsch-Jozsa algorithm and a quantum computer you would just need one evaluation of the oracle. There are a lot of great explanations of how this works, including the Quantum Katas tutorials. I really think this should be the first one you should try to really understand. It’s definitely simpler that Shor’s or Grover’s algorithms.
The Quantum Teleportation is often depicted to be the Hello World of quantum programming. However, Deutsch-Jozsa is the algorithm that will really give you the intuition on why the quantum computing provides these incredible algorithmic speedups. If you are interesting on a well explained blog post about Quantum Teleportation, I would recommend this one.
That’s all for this onboarding tour and tips compilation. I hope that you are now really excited to give a try to Quantum Katas. Happy quantum coding!
